就从最简单的线性回归模型（Linear Regression model）开始学习吧。

从这个模型的名字我们可以看出，因变量和变量之间的关系是线性的，预测值可以通过计算输入特征的权重给出：

其中，$\hat{y}$是预测值，$n$是特征数量，$\theta_0$是bias，$x_i$是第$i$个特征值，$\theta_j$是第$j$个特征的模型参数。如果获取了模型的所有参数，给定一个样本我们就可以用上面这个公式模型得到预测值。
为了表达更简洁，一般用向量表示：

其中$h_{\mathbf{\theta}}()$是hypothesis function是关于$\mathbf{\theta}$的假设函数，$\mathbf{\theta} = [\theta_0;\theta_1;…;\theta_n]$，$\mathbf{x} = [x_0, x_1, x_2, …, x_n]$并且$x_0=1$。
我们的目标当然是想要所有预测值都跟实际值相等，因此，目标函数或者称代价函数建模为：

其中$\mathbf{X}$为所有样本的集合，数量为$m$。

标准闭式解

基于均方误差最小化来进行模型求解的方法称为“最小二乘法”（least square method）。在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和最小。
一般地，我们利用最小二乘法对$\mathbf{\theta}$进行估计。数据集$\mathbf{X}$表示为：

然后把实际值也写成向量模式$\mathbf{y}=(y_1;y_2;…;y_m)$，因此优化问题为：

令$E_{\mathbf{\theta}}=(\mathbf{y}-\mathbf{\theta}^T\mathbf{X})^T(\mathbf{y}-\mathbf{\theta}^T\mathbf{X})$，对$\mathbf{\theta}$求导可得：

令上式等于0可解得

如果$\mathbf{X}^T\mathbf{X}$不可逆怎么办，这可能是由于矩阵中存在冗余特征，在线性代数里说明矩阵并非线性不相关，因此可以删除多余特征；也有可能是由于特征数大于等于样本数，也就是$m \le n$，可以通过删除一些特征或者使用正则化（regularization，后续介绍）。
给出python一个实现例子如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

import numpy as np 

X = 2 * np.random.rand(100, 1)
y = 2 + 6 * X + np.random.randn(100, 1)

X_b = np.c_[np.ones((100, 1)), X] # add x0 = 1 to each instance
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print(theta_best)
# [[1.74568681] [6.27246194]]

X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new] # add x0 = 1 to each instance
y_predict = X_new_b.dot(theta_best)
print(y_predict) #[[ 1.74568681] [14.29061069]]

plt.plot(X_new, y_predict, "r-")
plt.plot(X, y, "b.")
plt.axis([0, 2, 0, 15])
plt.show()

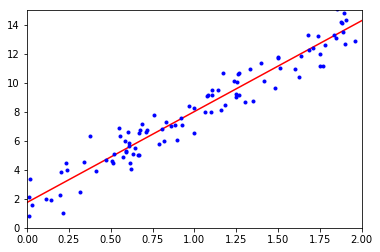
如果用sklearn实现的话，代码如下：

1
2
3
4
5
6
7
8

>>> from sklearn.linear_model import LinearRegression
>>> lin_reg = LinearRegression()
>>> lin_reg.fit(X, y)
>>> lin_reg.intercept_, lin_reg.coef_
(array([ 4.21509616]), array([[ 2.77011339]]))
>>> lin_reg.predict(X_new)
array([[ 4.21509616],
[ 9.75532293]])

这种方式实现的计算复杂度只要在矩阵求逆上，对于一个$n \times n$的矩阵，求逆复杂度大约是$O(n^{2.4})$到$O(n^{3})$，当特征数量很大时（比如100,000以上时），标准闭式解会变得很慢；另一方面，对于样本数量其复杂度是$O(m)$，也就是线性的；此外，模型训练完成后，预测的复杂度对于样本数量和特征数量复杂度都很快。

梯度下降法

梯度下降法是十分常用的优化算法，目的是通过迭代过程不断更新参数进而最小化代价函数，每次优化的方向都是斜率绝对值最大的方向。
Note：

• 需要谨慎选择步长（step size）或者叫做学习率（learning rate），太小的话，需要许多次迭代才能走到最优点，而步子太大，则有可能跨过最优点，然后陷入震荡。
• 凸优化问题找到最优点比较容易，而非凸问题则容易陷入局部最优点或者陷入平台（plateau)。线性回归问题是个凸优化问题。
• 最好在使用梯度下降法前对数据进行标准化处理，不然“碗”太长需要更多的迭代次数。
• 问题参数越多，维度越大，参数空间越大，搜索最优解也就越难。

Batch Gradient Descent

Batch是批的意思，批梯度下降就是在每次迭代过程中把所有数据都来计算代价函数的偏导，也就是梯度。代价函数对于参数$\theta_j$的偏导为：

用向量来表示梯度下降为：

由此，我们可以得到梯度下降的步骤：

推导出这个公式之后就可以实现了：

1
2
3
4
5
6
7

eta = 0.1 # learning rate
n_iterations = 1000
m = 100
theta = np.random.randn(2,1) # random initialization
for iteration in range(n_iterations):
	gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
	theta = theta - eta * gradients

Stochastic Gradient Descent

在前面讲过，BGD在每次迭代中是把所有数据都用于计算的，因此当数据量很大时，算法会变得难以忍受的慢，因此需要使用其他梯度下降算法。随机梯度下降法跟批梯度下降是两个极端，SGD在每次迭代中会随机从训练集中选择一个样本，然后只用这个样本计算并更新梯度。因此，这个算法计算比BGD快很多很多；但也由于其随机特性，优化曲线不会“直接”向着最优点前进，而是来回波动，但最终会抵达最优值附近。其算法如下图所示：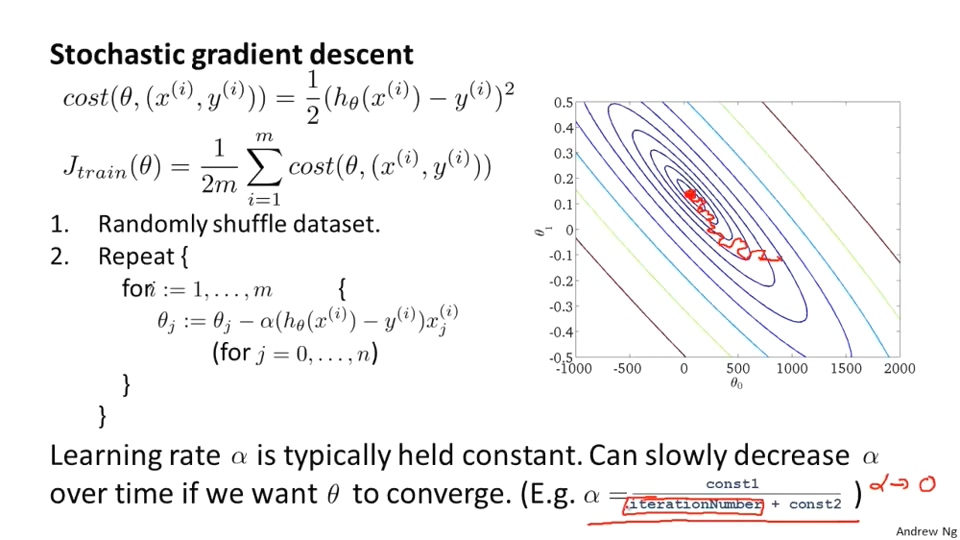

Python实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

n_epochs = 50
t0, t1 = 5, 50 # learning schedule hyperparameters
def learning_schedule(t):
return t0 / (t + t1)
theta = np.random.randn(2,1) # random initialization
for epoch in range(n_epochs):
	for i in range(m):
		random_index = np.random.randint(m)
		xi = X_b[random_index:random_index+1]
        yi = y[random_index:random_index+1]
        gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
        eta = learning_schedule(epoch * m + i)
        theta = theta - eta * gradients
print(theta)

如果用sklearn来实现的话，代码就简单多了：

1
2
3
4

from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(n_iter=50, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel())
print(sgd_reg.intercept_, sgd_reg.coef_)

NOTE: epoch是指把所有数据样本都遍历一遍，iteration表示更新一次参数，batch则是指数据样本的大小，在SGD中，iteration=batch=1，epoch=num_X/batch

Mini-batch Gradient Descent

Mini-batch GD介于SGD和BGD之间，也就是每次用来更新参数的样本不是一也不是所有（吴恩达说在2-400之间，他倾向于用10），它吸收了BGD和SGD的优缺点的折中，收敛更快，随机性较小，但也难抵达最优值，其算法流程如下图所示：

这里介绍的标准闭式解只适用于线性回归问题，但梯度下降法可以用来训练许多模型，在深度学习中也有广泛应用，将他们比较如下：

Polynomial Regression

如果数据并非一条直线呢，那么还可以用线性模型吗？实际上是可以的，主要方法就是把一个特征拓展成多维的，比如$x^2, x^3,…, x^k$，然后将其作为另一个维度的特征，比如$x_1 = x, x_2 = x^2$，那么就可以用线性模型按照上面的方法进行训练了，用sklearn实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 1 * X**2 + X + 2 + np.random.randn(m, 1)
plt.scatter(X, y)

poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
print(lin_reg.intercept_, lin_reg.coef_)
xx = np.array((range(-3, 4)))
print(xx)
yy = xx*0.98134428+xx*xx*0.94365742+1.94555083
plt.plot(xx, yy, c='r')
plt.show()

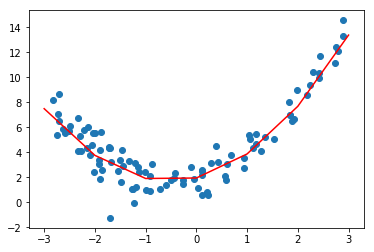
此外，需要注意，PolynomialFeatures(degree=d)会把一个包含n个特征的矩阵转化为包含$\frac{(n+d)!}{d!n!}$个特征的矩阵，即如果对于两个特征a和b，令degree=3，那么特征不仅有$a^2$，$a^3$，$b^2$，$b^3$，还会有$ab$，$a^2b$和$ab^2$.