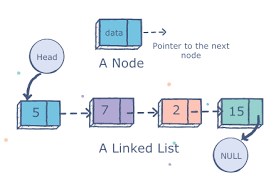
链表的算法合集大全(C/C++)
1. 链表结构体定义
1
2
3
4
5
6
7
| struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};
|
2. 链表初始化,可以快速创建样例
1
2
3
4
5
6
7
8
9
10
11
12
13
| // 链表初始化,创造样例
ListNode* linkedListInit(vector<int> v) {
if (v.empty()) return NULL;
ListNode* root = new ListNode(v[0]);
ListNode* node = root;
int i = 1;
while (i<v.size()) {
node->next = new ListNode(v[i]);
node = node->next;
i++;
}
return root;
}
|
3. 链表遍历打印,检验算法正确性
1
2
3
4
5
6
7
8
9
| // 打印链表元素值,检验算法
void PrintLinkedList(ListNode* root) {
if (root == NULL) return;
while (root != NULL) {
cout<<root->val<<" ";
root = root->next;
}
cout<<endl;
}
|
4. 输出单链表倒数第 K 个节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| // 输出单链表倒数第 K 个节点
// 法一:两次遍历
ListNode* findKthTail1(ListNode *pHead, int k) {
if (pHead == NULL || k <= 0) return NULL;
int len = 0;
ListNode* root = pHead;
while (pHead != NULL) {
pHead = pHead->next;
len++;
}
if (len<k) return NULL;
int countdown = len-k;
while (countdown-->0) {
root = root->next;
}
return root;
}
// 法二:递归**
int cnt = 0;
ListNode* findKthTail2(ListNode* pHead, int k) {
if (pHead == NULL) return NULL;
ListNode* node = findKthTail2(pHead->next, k);
// 没找到就返回NULL,找到一直返回结点
if (node == NULL) {
cnt++;
if (cnt == k) return pHead;
else return NULL;
}
else {
return node;
}
}
// 法三:快慢指针***
ListNode* findKthTail3(ListNode* pHead, int k) {
if (pHead == NULL || k <= 0) return NULL;
ListNode* slow = pHead;
ListNode* fast = pHead;
for(int i=0;i<k;i++) { //快指针先走k步
if(fast) fast = fast->next;
else return NULL;
}
while(fast) {
fast = fast->next;
slow = slow->next;
}
return slow;
}
|
5. 判断链表是否有环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| // 判断链表是否有环
// 法一:穷举比较 O(n^2)
// 法二:哈希缓存 O(n)
// 法三:快慢指针 O(n)~O(n^2)环很大时
bool isExistRing3(ListNode* pHead) {
if (pHead == NULL) return false;
ListNode* fast = pHead;
ListNode* slow = pHead;
while (fast->next && slow) {
fast = fast->next->next;
slow = slow->next;
if (fast == slow) return true;
}
return false;
}
|
6. 定位环的入口
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| // 定位环的入口***hard***
ListNode* getEntryNodeOfRing(ListNode* pHead) {
ListNode* meetingnode = getMeetingNode(pHead);
if (meetingnode == NULL) return NULL; // 没环则相遇尾结点
ListNode* p1 = meetingnode;
ListNode* p2 = pHead;
// p1和p2以相同的速度向前移动,当p2指向环的入口节点时
// p1已经围绕着环走了n圈又回到了入口节点。
while(p1 != p2) {
p1 = p1->next;
p2 = p2->next;
}
return p1;
}
ListNode* getMeetingNode(ListNode* pHead) {
if (pHead == NULL) return NULL;
ListNode* fast = pHead;
ListNode* slow = pHead;
while (fast->next && slow) {
fast = fast->next->next;
slow = slow->next;
if (fast == slow) return slow;
}
return NULL;
}
|
7. 计算环的长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| // 计算环的长度
// 找到slow与fast的相遇节点,令slow与fast指针从相遇节点出发,
// 按照之前的前进规则,当slow与fast再次相遇时,slow走过的长度正好为环的长度。
int getLengthOfRing(ListNode* pHead) {
if (pHead == NULL) return 0;
ListNode* meetingnode = getMeetingNode(pHead);
if (meetingnode == NULL) return 0; // 防止无环
ListNode* fast = meetingnode->next->next;
ListNode* slow = meetingnode->next;
int length = 1;
while (fast != slow) {
fast = fast->next->next;
slow = slow->next;
}
return length;
}
|
8. 链表实现大数加法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| // 链表实现大数加法
ListNode* numberAddAsList(ListNode* l1, ListNode* l2) {
ListNode *ret = l1, *pre = l2;
int up = 0; // 进位
while (l1 != NULL && l2 != NULL) {
l1->val = l1->val + l2->val +up;
up = l1->val / 10;
l1->val %= 10;
pre = l1; //记录当前结点位置
l1 = l1->next;
l2 = l2->next;
}
// 若l1到达末尾,说明l1长度小于l2
if (l1 == NULL) {
pre->next = l2; // pre->next指向l2当前位置
}
l1 = pre->next; // l1指针指向l2结点当前位置,即把l2拼到l1上继续计算
// 继续计算剩余结点,防止9999999+1这种情况
while (l1 != NULL) {
l1->val = l1->val + up;
up = l1->val / 10;
l1->val %= 10;
pre = l1;
l1 = l1->next;
}
// 最高位有进位,新建一个结点保留最高位
if (up != 0) {
ListNode* tmp = new ListNode(up);
pre->next = tmp;
}
return ret;
}
|
9. 有序链表合并
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| // 有序链表合并
// 递归
ListNode* mergeTwoOrderedListsRec(ListNode* pHead1, ListNode* pHead2){
if(pHead1 == NULL) return pHead2;
if(pHead2 == NULL) return pHead1;
if(pHead1->val > pHead2->val) {
pHead2->next = mergeTwoOrderedListsRec(pHead1, pHead2->next);
return pHead2;
}
else {
pHead1->next = mergeTwoOrderedListsRec(pHead1->next, pHead2);
return pHead1;
}
}
// 非递归
ListNode* mergeTwoOrderedListsNotRec(ListNode* pHead1, ListNode* pHead2) {
if (pHead1 == NULL) return pHead2;
else if (pHead2 == NULL) return pHead1;
else {
ListNode* pTail = NULL; // 新链表最后一个结点
ListNode* newHead = NULL; // 合并后链表第一个结点
if (pHead1->val < pHead2->val) {
newHead = pHead1;
pHead1 = pHead1->next;
}
else {
newHead = pHead2;
pHead2 = pHead2->next;
}
pTail = newHead; // 指向第一个结点
while (pHead1 && pHead2) {
if (pHead1->val <= pHead2->val) {
pTail->next = pHead1;
pHead1 = pHead1->next;
}
else {
pTail->next = pHead2;
pHead2 = pHead2->next;
}
pTail = pTail->next;
}
if (pHead1 == NULL) pTail->next = pHead2;
else if (pHead2 == NULL) pTail->next = pHead1;
return newHead;
}
}
|
10. K个有序链表合并
1
2
3
4
5
6
7
8
9
10
11
12
13
| // K个有序链表合并
// 归并排序,复杂度O(nlogk)
ListNode* mergeKsortedLists(vector<ListNode*> lists) {
int amount = lists.size();
int gap = 1;
while (gap < amount) {
for (int i=0; i< amount-gap; i+=gap*2) {
lists[i] = mergeTwoOrderedListsRec(lists[i], lists[i+gap]);
}
gap *= 2;
}
return amount>0?lists[0]:NULL;
}
|
11. O(1)复杂度删除链表中结点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| void deleteNode(ListNode **pHead, ListNode* pDelNode) {
if (pDelNode == NULL) return;
if (pDelNode->next != NULL) {
ListNode* pNext = pDelNode->next;
// 下一个节点的值赋给删除节点
pDelNode->val = pNext->val;
pDelNode->next = pNext->next;
delete pNext; // delete是删除指针指向的内容
pNext = NULL; // 不指向NULL会成为野指针
}
else if (*pHead == pDelNode) { //头结点
delete pDelNode;
pDelNode = NULL;
*pHead = NULL;
}
else { //删除尾结点
ListNode *pNode = *pHead;
while (pNode->next != pDelNode) {
pNode = pNode->next;
}
pNode->next = NULL;
delete pDelNode;
pDelNode = NULL;
}
}
|
12. 从尾到头打印链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| // 递归
vector<int> printListFromTailToHead1(ListNode* head) {
vector<int> res;
if(head!=NULL){
if(head->next!=NULL){
res = printListFromTailToHead1(head->next);
}
res.push_back(head->val);
}
return res;
}
//栈
vector<int> printListFromTailToHead2(ListNode* head) {
vector<int> res;
stack<int> sta;
while(head!=NULL){
sta.push(head->val);
head=head->next;
}
while(!sta.empty()){
res.push_back(sta.top());
sta.pop();
}
return res;
}
// **链表原地反转**
vector<int> printListFromTailToHead3(struct ListNode* head) {
vector<int> vec;
ListNode *buf=head;
ListNode *pre=buf;
if(head==NULL)
return vec;
while(head->next!=NULL){ /*这里还没看懂*/
buf=head->next;
head->next=buf->next;
buf->next=pre;
pre=buf;
}
while(buf){
vec.push_back(buf->val);
buf=buf->next;
}
return vec;
}
|
13. 反转链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| // 迭代(链表的原地反转)
ListNode* reverseList1(ListNode* head) {
ListNode* pre = NULL;
ListNode* cur = head;
while (cur != NULL) {
ListNode* next = cur->next;
cur->next = pre;
pre = cur;
cur = next;
}
return pre;
}
// 递归
ListNode* reverseList2(ListNode* head) {
if (head == NULL || head->next == NULL) {
return head;
}
ListNode* rhead = reverseList2(head->next);
// head->next此刻指向head后面的链表的尾节点
// head->next->next = head把head节点放在了尾部
head->next->next = head;
head->next = NULL;
return rhead;
}
|
14. 复杂链表的复制
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| // (每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针
// 指向任意一个节点),返回结果为复制后复杂链表的head。
RandomListNode* Clone(RandomListNode* pHead){
if(pHead==NULL) return NULL;
RandomListNode* currentNode=pHead;
//复制每个结点,将其插入结点后面
while(currentNode!=NULL){
RandomListNode* cloneNode = new RandomListNode(currentNode->label);
RandomListNode* nextNode = currentNode->next;
currentNode->next=cloneNode;
cloneNode->next=nextNode;
currentNode=nextNode;
}
currentNode=pHead;
//复制老结点的随机指针给新结点
while(currentNode!=NULL){
currentNode->next->random = currentNode->random==NULL?NULL:currentNode->random->next;
currentNode=currentNode->next->next;
}
//拆分链表
currentNode=pHead;
RandomListNode* pCloneHead=pHead->next;
while(currentNode!=NULL){
RandomListNode* cloneNode=currentNode->next;
currentNode->next=cloneNode->next;
cloneNode->next=cloneNode->next==NULL?NULL:cloneNode->next->next;
currentNode=currentNode->next;
}
return pCloneHead;
}
|
15. 逆序构造单链表
输入数据:[1,2,3,4,5],构造单链表:5->4->3->2->1
1
2
3
4
5
6
7
8
9
10
11
| // 逆序构造单链表
ListNode* desc_construct(vector<int> input) {
if (input.empty()) return NULL;
ListNode* pre = NULL;
for (int i=0;i<input.size();i++) {
ListNode* cur = new ListNode(input[i]);
cur->next = pre;
pre = cur;
}
return pre;
}
|
16. 链表升序排序
快排是需要一个指针指向头,一个指针指向尾,然后两个指针相向运动并按一定规律交换值,最后使得支点左边小于支点,支点右边大于支点,但是对于单链表而言,指向结尾的指针很好办,但是这个指针如何往前,我们只有一个 next(这并不是一个双向链表)。
我们只需要两个指针 i 和 j,这两个指针均往 next 方向移动,移动的过程中始终保持区间 [1, i] 的 data 都小于 base(位置 0 是主元),区间 [i+1, j) 的 data 都大于等于 base,那么当 j 走到末尾的时候便完成了一次支点的寻找。若以 swap 操作即 if 判断语句成立作为基本操作,其操作数和快速排序相同,故该方法的平均时间复杂度亦为$T(n) = O(nlogn)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| // 链表升序排序
/**
* @param begin 链表的第一个结点,即header->next
* @param end 链表的最后一个结点的next
*/
void asc_sort(ListNode* begin, ListNode* end) {
// 链表为空或只有一个结点
if (begin == end || begin->next == end) return;
int base = begin->val;
ListNode* i = begin;
ListNode* j = begin->next;
while (j != end) {
if (j->val < base) {
i = i->next;
swap(i->val, j->val);
}
j = j->next;
}
swap (i->val, begin->val);
asc_sort(begin, i);
asc_sort(i->next, end);
}
// usage: asc_sort(header->next, nullptr);
|
17. 找出单链表的中间结点
1
2
3
4
5
6
7
8
9
10
11
12
| // 找出单链表的中间结点(类似倒数第k个结点)
// 法一:遍历一次,再遍历到n/2,复杂度为O(n+n/2)
// 法二:快慢指针
ListNode* find_middle(ListNode* head) {
ListNode* fast = head;
ListNode* slow = head;
while (fast->next && fast->next->next) {
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
|