智能优化算法（2）：蚁群算法

1.2 蚁群优化算法

蚁群优化（Ant Colony Optimization, ACO）算法是源自大自然生物界的仿真类算法，其思想吸收了蚁群觅食过程中的行为特性。蚁群算法在TSP问题、二次分配问题、图着色问题、车辆调度问题、通信网络中的负载均衡问题等表现出良好的优化性能。

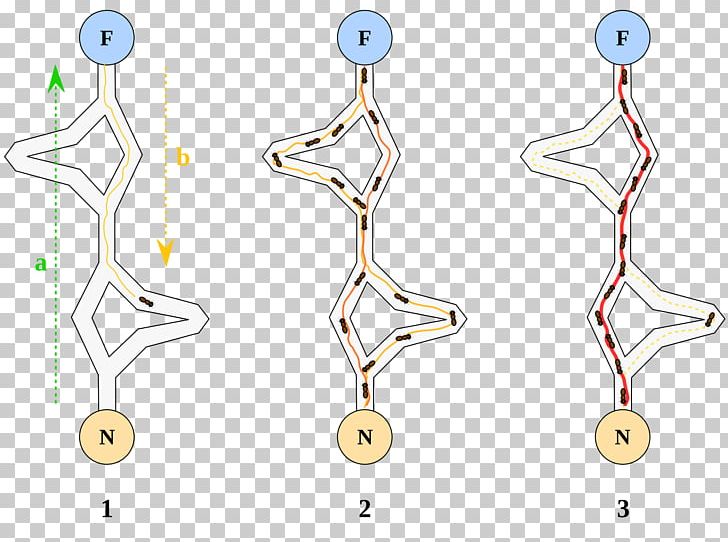
大自然中的蚂蚁没有视觉，依赖于同类散发在环境中的信息素决定自己何去何从，孤立的蚂蚁沿着同伴的信息素轨迹移动，同时释放自己的信息素，从而增强了该路线上的信息素数量，随着越来越多的蚂蚁通过该路线，一条较佳的路线就形成了（这条路径不一定最短，但对于NP-hard问题而言足够了）。

1.2.1 算法模型

以旅行商问题（Traveling Salesman Problem, TSP）为例，在图论中称为最小Hamilton问题。

记$G = (V,E)$为赋权图，$V=(1,2,3,…,N)$为顶点集，$E$为边集，各顶点间的距离$d_{ij}$已知$(d_{ij}>0,d_{ii}=\infty,i,j\in V)$，设

则经典的TSP问题可以表示如下：

服从如下几个约束：

• 约束1：$\sum_{j=1}^{n}x_{ij}=1, i\in V$
• 约束2：$\sum_{i=1}^{n}x_{ij}=1, j\in V$
• 约束3：$\sum_{i\in S}\sum_{j\in S}x_{ij} \le |S|-1, \forall S \subset V$
• 约束4：$x_{ij}\in \{0, 1\}$

其中$|S|$为集合中所含图的顶点数；约束1和2对于每个点来说只有一条边进一条边出，也就是任意两个点间只有一条最优路线；约束3保证了没有任何子回路的产生。

当$d_{ij} = d_{ji}$时，问题被称为对称型TSP；当对于所有$1\le i, j,k \le n$时，有不等式$d_{ij}+d_{jk}\ge d_{ik}$成立，问题被称为是满足三角形不等式的，记为$\Delta$TSP。三角形不等式在很多情况下是满足的，即使不满足也可以转换为闭包形式求等价TSP最优解。

蚁群优化算法基本模型：

1. 蚂蚁群体总是寻找最小费用可行解
2. 蚂蚁具有记忆性，存储当前路径的信息，构造可行解、评价解的质量、路径反向追踪
3. 当前状态的蚂蚁可以移动到可行领域任意一点
4. 每个蚂蚁赋予一个初始状态和若干个终止条件
5. 蚂蚁从初始状态到可行领域状态，以递推方式构造解，当有一个蚂蚁满足至少一个终止条件时构造过程结束
6. 蚂蚁按某种概率决策规则移动至领域结点
7. 移动后信息素轨迹被更新，过程称为“单步在线信息素更新”
8. 一旦构造出一个解，蚂蚁沿原路方向追踪，更新信息素轨迹，称为“在线延迟信息素更新”

1.2.2 算法分析

算法复杂度是$O(nc\cdot n^2\cdot m)$，m为蚂蚁个数，nc为迭代次数或者搜索次数，n为顶点数。算法运行效果受到$\alpha, \beta$等参数影响，其中$\beta$的影响在于体现信息素轨迹的持久性，数值过小意味着信息消失过快；数值过大容易落入局部最优点，因此其数值通常取0.7左右。

在基本的蚁群优化算法上，可以与其他启发式算法相结合，最典型的就是嵌入局部搜索算法，在各个蚂蚁形成自己的路线后，用局部调整方法（2-opt, 3-opt）加以改进，此外，与遗传算法、模拟退火和禁忌搜索等结合也有一定的成效。

混合蚁群优化算法主要步骤：

1. Begin
2. 蚂蚁初始化；
3. LOOP：
4. $\quad$蚂蚁路径构造；
5. $\quad$对某个蚂蚁实施局部搜索算法
6. $\quad$蚂蚁轨迹更新
7. $\quad$若迭代次数未到，转LOOP；
8. 输出当前最好解
9. End