3.2 差分进化算法
差分进化(Differential Evolution, DE)算法是在求解Chebyshev多项式拟合问题时提出的,算法主要通过基于差分形式的变异操作和基于概率选择的交叉操作进行优化搜索。DE算法最初的设计方法源于遗传退火算法,主要操作包括变异、交叉和选择,但具体实现方法与遗传算法有本质区别。
3.2.1 算法原理
算法首先对搜索群体进行初始化。假设$NP$表示群体规模,$D$表示变量维数,$G$表示迭代次数,令$X_{i,G}$表示第$G$代的寻优个体$i$,并可以表示为:
对每个搜索个体的解采用随机初始化方法,例如个体$i$的第$j$个解的分量可以通过如下方法产生:
其中$X_{\max}^j$和$X_{\min}^j$分别表示第$j$个分量的上下界;$r$表示在[0,1]间服从均匀分布的随机数。完成初始化后,进入循环
1. 变异操作
在DE算法中,经典的变异操作是在目标向量的基础上,利用两个向量的差分进行解的更新,比如:
其中$r_1,r_2,r_3$是从当前搜索群体中随机选择的三个个体编号,要求$r_1\ne r_2 \ne r_3$;$X_{i,G}$称为目标向量;$V_{i,G}$表示个体$X_{i,G}$变异后的解向量,称为个体i的合成向量;$X_{r_1,G}$表示被选择的进行变异的向量,$X_{r_2,G}$和$X_{r_3,G}$是被选择进行差分操作的两个向量;系数$F$称为缩放因子,用于控制差分向量对变异公式的影响。
2. 交叉操作
在DE算法中,交叉操作是利用合成向量$V_{i,G}$和目标向量$X_{i,G}$的分量进行重新组合产生试验向量$U_{i,G}$,以提高解的多样性。目前,二项式交叉和指数交叉是DE算法主要的交叉方法,二项式交叉对应定义如下:
其中,rand表示[0,1]之间服从均匀分布的随机数;Cr表示交叉概率,且取值与[0,1];$j_{rand}$表示在区间[1,D]上随机产生的整数。
指数交叉实现方法如下:
其中,$n$和$L$是在[1,D]上随机产生的整数;$<>_D$表示对D进行取模运算。
3. 选择操作
选择操作是基于贪婪策略,比较试验向量$U_{i,G}$和目标向量$X_{i,G}$的优劣,挑选更优的值作为下一代的目标向量。
DE算法的流程如下图所示: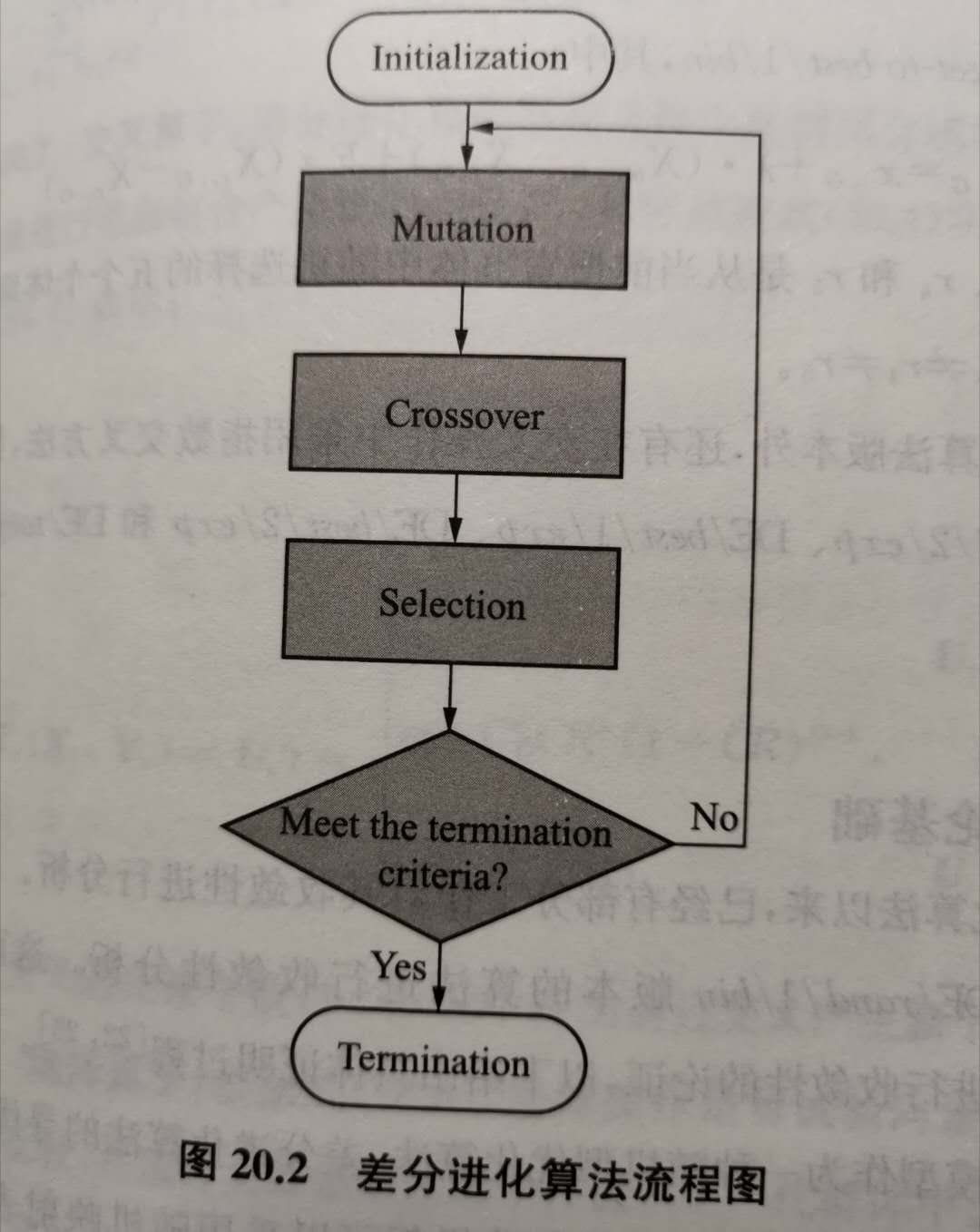
上述算法是差分优化算法的基本形式,目前还有其他版本的算法,可以用DE$/x/y/z$表示,其中$x$表示被变异的向量选择方法;$y$表示变异种采用的差分向量的个数;$z$表示交叉操作的方法,上bin表示二项式交叉,exp表示指数交叉,因此前面的DE算法可以表示为DE$/rand/1/bin$,此外,其他DE算法的形式有:
- DE$/rand/2/bin$
- DE$/best/1/bin$
- DE$/best/2/bin$
- DE$/target-to-best/1/bin$
- DE$/rand/1/exp$
3.2.2 应用案例
瓶颈TSP问题(不追求总巡回路线最短,希望在巡回路线中单次行程尽可能短)、Chebyshev多项式拟合问题