1.3 微粒群优化算法
微粒群优化(Particle Swarm Optimization, PSO)算法,或称为粒子群优化算法,是一种基于鸟群觅食行为规律提出的群体智能优化算法。算法概念简明,易于实现。
在群体觅食过程中,群体中的每一个个体都会受益于所有成员在这个过程中发现和积累的经验。而基于信息交流和共享的个体检的协作正式微粒群优化算法进行优化搜索的基础。
微粒群算法模拟鸟类觅食模型,将优化问题的搜搜空间类比作鸟类的飞行空间,所需要找到的最优解相当于食物,算法将每只鸟抽象为没有质量的微粒,每个微粒有位置和速度两个特征向量,位置代表候选解,解的优劣通过适应度函数大小进行评价;微粒速度决定飞行方向和速率。
优化过程中,微粒和位置和其他算法一样需要随机初始化,通过迭代进行更新,每次迭代需要通过两个极值进行更新,第一个是每个微粒当前所找到的最好的解,称为个体极值;第二个极值是整个群体找到的最好的解,称为全局极值。每个微粒根据自身经验和群体经验进行更新。
1.3.1 算法模型
设待求解的优化问题维度为$N$,微粒群体规模为$M$,在微粒群优化算法中,$x_i = (x_{i1}, x_{i2}, x_{i3}, …, x_{iN})$表示第$i$个微粒的位置;$v_i=(v_{i1},v_{i2},…,v_{iN})$表示第$i$个微粒的速度;$p_i=(p_{i1},p_{i2},…,p_{iN})$表示第$i$个微粒所搜寻到的最好的位置;$g_i=(g_{1},g_{2},…,g_{N})$表示整个群体所搜寻到的最好的位置。
Eberhart和Kennedy最初提出的基本微粒群优化算法采用如下迭代方程进行速度和位置的更新:
其中,$i=1,2,…,M;d=1,2,…,N;c_1$和$c_2$是学习因子;$t$表示迭代次数;$r_1$和$r_2$是在$[0,1]$上服从均匀分布的随机数。
在速度更新方程中,第一项表示微粒根据自身的速度进行惯性运动;第二项表示微粒根据自身经验进行调整,称为认知部分;第三项表示微粒根据其他微粒的经验进行调整,称为社会部分。需要指出的是,为了防止微粒的速度过大或者过小,需要限定速度的范围:
在求解边界约束问题上,如果更新后位置越界,常见的修正方法是将其限定在边界上。在公式1中,$g$是整个群体的最好位置。上述算法称为微粒群优化算法的全局版本;此外,也可以将微粒领域内的最好位置设为$g$,则称为局部版本;全局版本算法优化速度快,但是容易陷入局部最优;而局部版本算法优化速度慢,但容易找到更优解。
算法基本流程: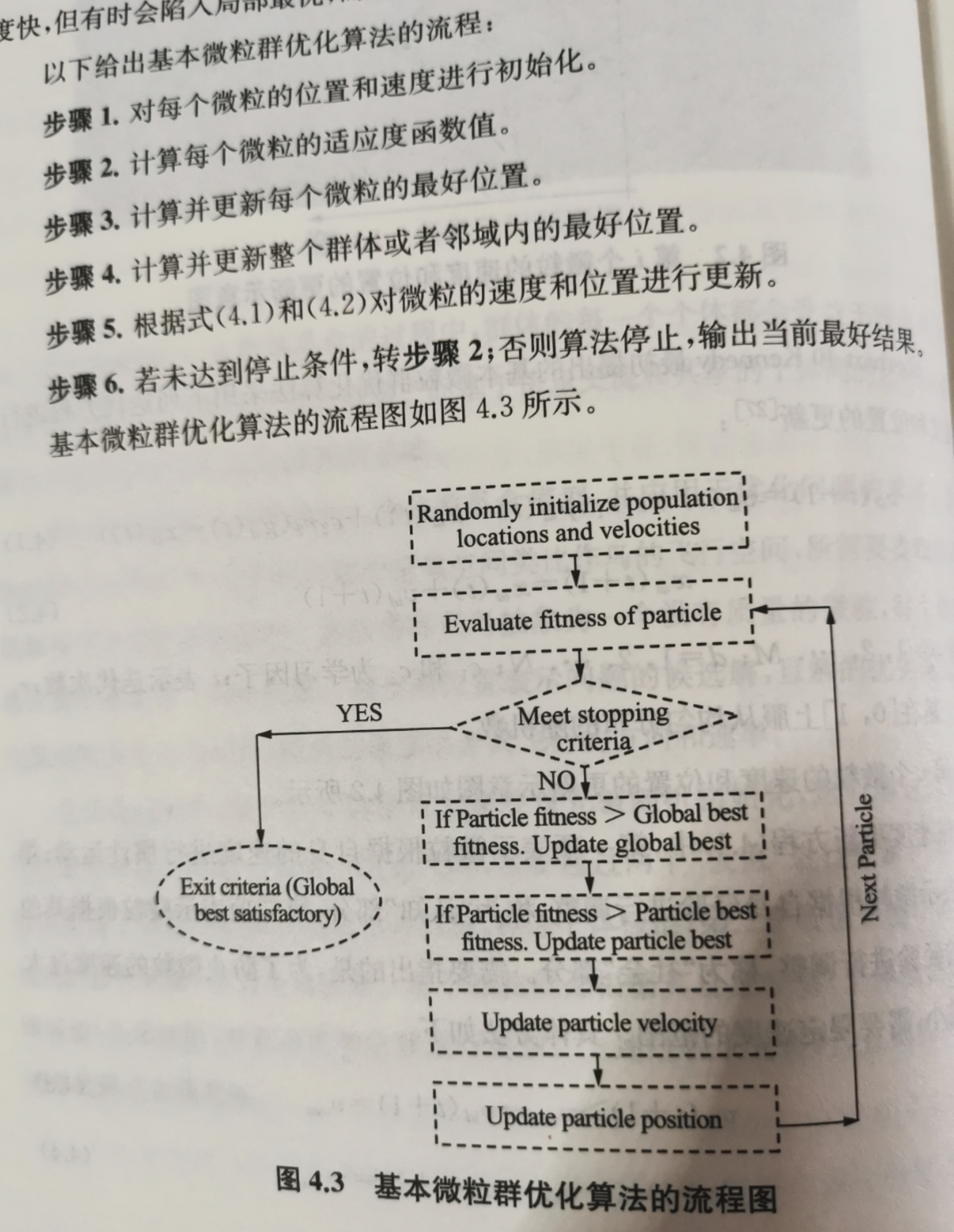
1.3.2 算法分析
学习因子
学习因子$c_1_$和$c_2$是微粒根据自身经验和社会经验对其运动进行更新的权重。如果令$c_1$为0,那么微粒缺乏自身经验,这是算法的优化速度可能比较快,但容易陷入局部极值;如果令$c_2$为0,那么优化信息无法在群体内传播,微粒搜索到最优解的概率非常低;如果同时为0,那么算法优化性能会急剧下降。
领域拓扑结构
微粒群间的信息交流是算法的重要组成部分,通过为止共享,每个微粒能够向比自身位置更好的方向运动,而领域拓扑就决定了信息交流的方向。拓扑类型有:
- 环型(每个微粒受近邻影响,只向最好近邻位置运动)
- 星型(全局领域拓扑,完全图,计算复杂度较高)
- 齿型(发散的,中心向最好微粒逼近,再把经验传递给其他微粒,其他微粒两两不相连)
研究发现,环型拓扑收敛速度慢,容易找到全局最优解;星型拓扑收敛速度快,容易陷入局部极值;齿型拓扑优化效果差。这三种属于静态拓扑,还有动态拓扑——优化最小距离、逐步增长、重新组合。
在基本微粒群优化算法的基础上,有人提出了带惯性权重和收缩因子的两种算法版本:
惯性权重
其中$w$是惯性权重,用于对速度的控制;较大的惯性权重保证算法具有较强的全局探索能力,较小的惯性权重能保证算法具有较强的局部开发能力。目前,使惯性权重随迭代次数线性递减是最基本的策略,带惯性权重的优化算法是目前主流的算法版本。
收缩因子
其中收缩因子$\chi$是$c_1$和$c_2$的函数,函数表达式为:
其中$\mu = c_1+c_2>4$
1.3.3 应用案例
多目标优化