2.1 模拟退火算法
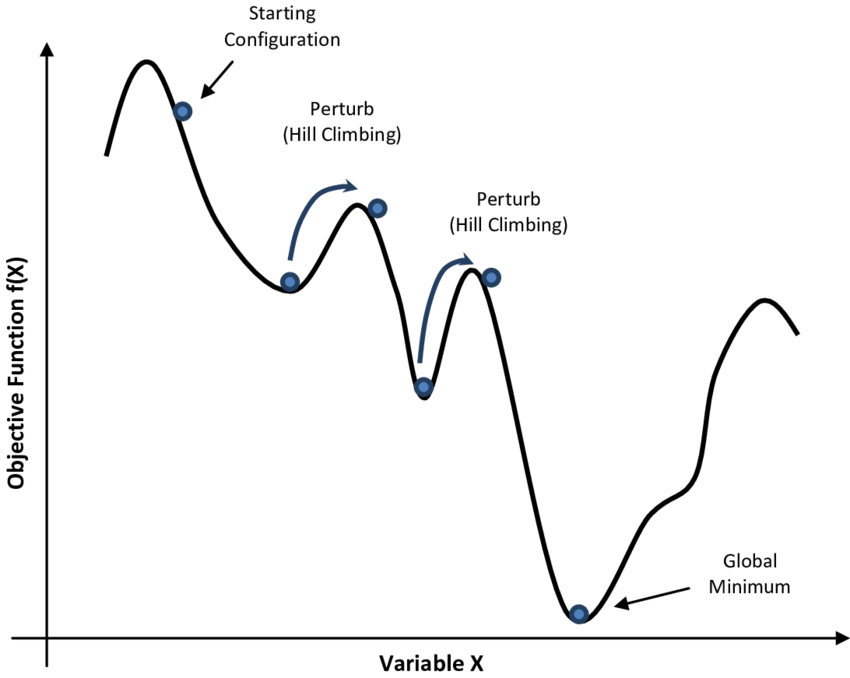
模拟退火(Simlated Annealing, SA)算法是一种全局搜索算法,是局部搜索算法的拓展。区别于其他算法,模拟退火算法不要求每次产生的新解质量都有提高。
2.1.1 算法原理
SA源于物理退火过程的模拟,在热力学和物理学中,将固体加温至融化状态,待其徐徐冷却之后使其凝固成规整晶体的过程称为物理退火,可以分为升温过程、降温过程和等温过程三个部分:
- 升温过程:加热过程中,温度不断升高,固体粒子热运动增强,能量也在增加;到熔点后固定融化为液态。粒子自由运动增加,从有序的结晶态转变为无序的液态,有助于消除固体内的非均匀态,使得随后的降温过程以某一平衡态为起点。
- 降温过程:在冷却时,温度慢慢降低,分子的热运动减弱,逐渐趋向有序。当温度到达结晶温度时,液体凝固,系统熵减小。在冷却时如果温度急剧降低物体只会冷凝为非均匀的亚稳态,系统能量也不会达到最小值。
- 等温过程:在物理退火中,系统在每一个温度下面达到平衡态的过程可以用封闭系统的等温过程来描述,即热力学系统在恒定温度下发生的各种物理或者化学过程。该过程可以保证每个温度下系统都能达到平衡态,最终达到固体的基态。
2.1.2 算法模型
在SA求解优化问题时,解和目标函数类似于退火过程中物体的状态和能量函数,而最优解就是物体达到能量最低的状态。
物理退火过程和模拟退火算法的对应关系
| 物理退火过程 | 模拟退火算法 |
| —— | —— |
| 系统状态 | 解 |
| 系统能量 | 目标函数 |
| 系统最低能量状态(基态)| 全局最优解|
| 加温过程 | 设置初始高温 |
| 降温过程 | 温度下降|
| 等温过程 | 基于Metropolis准则搜索 |
算法流程:
- 设置初始高温和终止温度,选择任意初始解$x$
- 内循环,在当前温度下随机产生一个邻域解$y\in N(x)$($N(x)$表示$x$的邻域),根据Metropolis准则,判断是否选择新解$y$。如此反复进行直到达到满足内循环停止条件。
- 外循环,若满足外循环终止条件算法停止
为达到每个温度下的平衡态,内循环次数要足够多,但在实际应用中无法达到理论上的平衡态,通常将内循环的次数设为常数值,在外循环中,通过调整温度来控制算法的搜索过程。
2.1.3 Metropolis准则
假设在温度$T$下,由当前状态$i$产生新的状态$j$,两种状态对应的能量分布为$E_i$和$E_j$,如果$E_i>E_j$,那么就接受新状态$j$。如果$E_i<E_j$,那么要根据系统处于新状态$j$的概率判断该状态是否为重要状态。上述概率用$r$表示,且
其中,$K_B$为Boltzman常数。
在[0,1]之间产生随机数$\xi$,如果$r>\xi$,那么新状态$j$为重要桩体,接受该状态,否则仍然保留状态$i$。
2.1.4 应用案例
平面选址问题,欧氏距离选址,绝对值选址