3.1 禁忌搜索算法
禁忌搜索(Tabu Search, TS)算法是局部搜索算法的拓展,采用禁忌表来记录已经到达过的局部最优点,使得在以后一段时期内的搜索中,不再重复搜索这些解,以此跳出局部极值点。
3.1.1 算法原理
区别于模拟退火算法通过温度调整算法从搜索空间的一个点移动到另一个点的概率来避免局部极值,在禁忌搜索算法中,是通过禁忌表驱动算法探索搜索空间的位置区域来避免早熟收敛。
局部最优解:给定一个最优化问题实例$(F, f)$的一个邻域$N$,一个可行解$x\in F$,若$\forall g \in N(x)$ 有 $f(x)\le f(g)$,称$x$为关于$N$的局部最优解。
邻域:对于组合优化问题$(D,F,f)$,其中$D$为所有解构成的状态空间,$F$为$D$上的可行域,$f$为目标函数,则一个邻域函数可定义为一种映射,即:
其中,$2^D$表示所有子集的集合,$N(x)$为$x$的邻域。
局部搜索算法本质上说是基于贪婪策略的搜索算法,容易实现,但是算法往往会陷入局部极值,无法保证获得全局最优解,为避免早熟收敛,禁忌搜索算法通过禁忌策略扩大寻优范围,提高算法全局优化能力。
3.1.2 算法模型
禁忌搜索算法第一次在优化过程中使用了记忆功能,使用禁忌表来避免重复搜索,扩大搜索区域。
1. 禁忌表
禁忌表由禁忌对象和禁忌长度组成,禁忌对象是产生解变化的因素,而禁忌长度是禁忌对象被禁次数。
禁忌对象分为解的简单变化、解向量分量变化、目标值变化
- 解的简单变化。从解空间中的$x$到$y$
- 解向量分量的变化。解向量有$n$维,其中一维或者某几维发生变化
- 目标值变化。具有相同目标值的解认为是同一状态,
2. 禁忌长度
禁忌长度就是被禁对象不允许被选择的迭代次数。
设置禁忌长度$t$的方法主要有两种:
- $t$为常数。
- $t$随迭代次数调整
研究表明,禁忌长度较大时,算法可以在更多的位置区域进行优化搜索,全局探索性能较好;禁忌长度较小时,算法可以进行精细搜索,局部开发能力较强。动态调整的禁忌长度比固定不变的禁忌长度能够让算法具有更好的性能。
3. 特设准则
优化过程中,可能会出现邻域解全是被禁对象,或者解禁某个对象后最优值发生改进。因此,可以将某个被禁对象解禁。
设置常用方法主要有以下几种:
- 基于评价值准则:如果邻域解的评价值优于历史当前最优值
- 基于最小错误原则:如果邻域解全是被禁对象,而且不满足评价值准则,那么可以从所有邻域解中选一个最优的
- 基于影响力准则:有些对象的变化对目标值影响较大
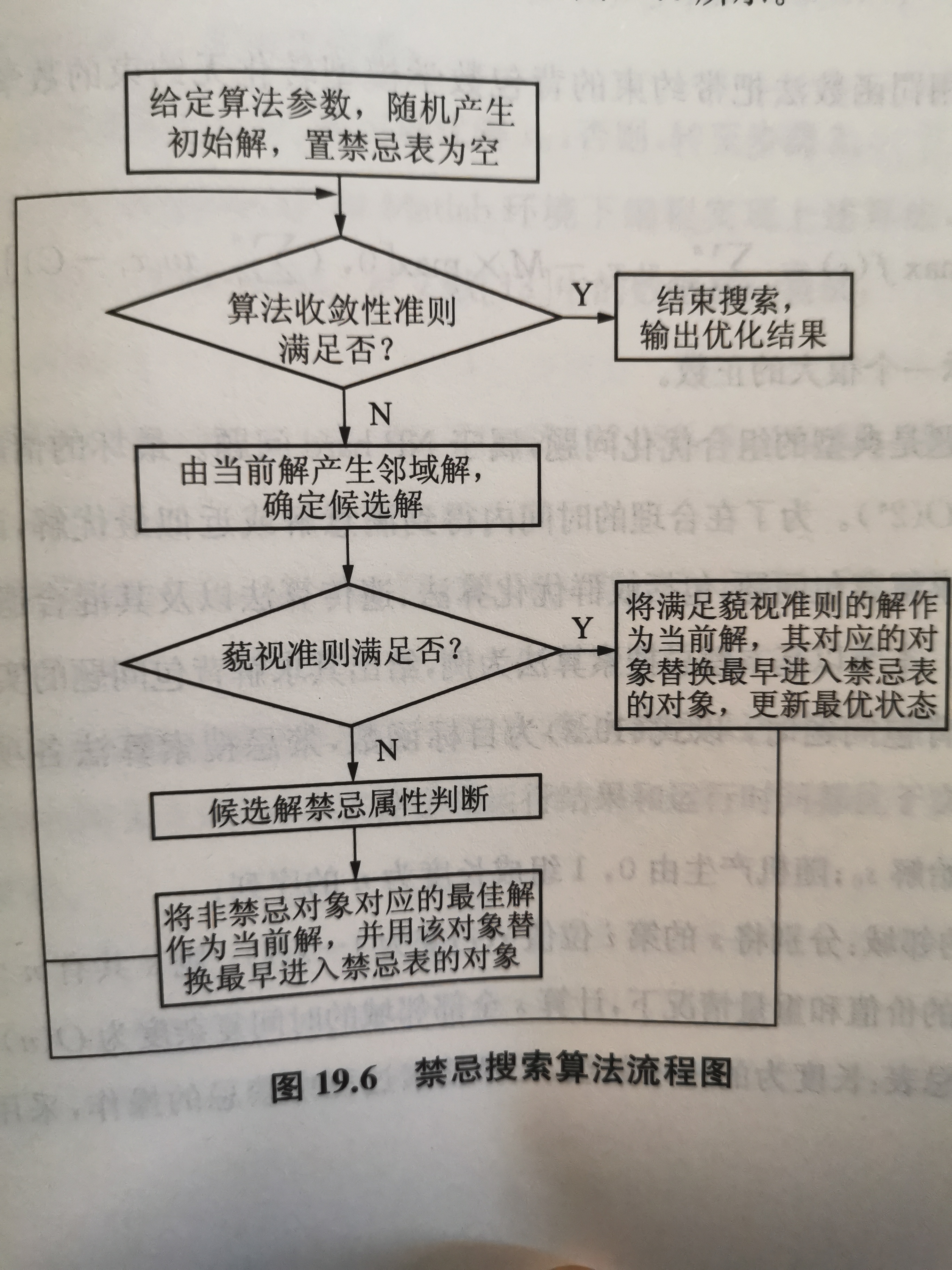
TS的流程图: