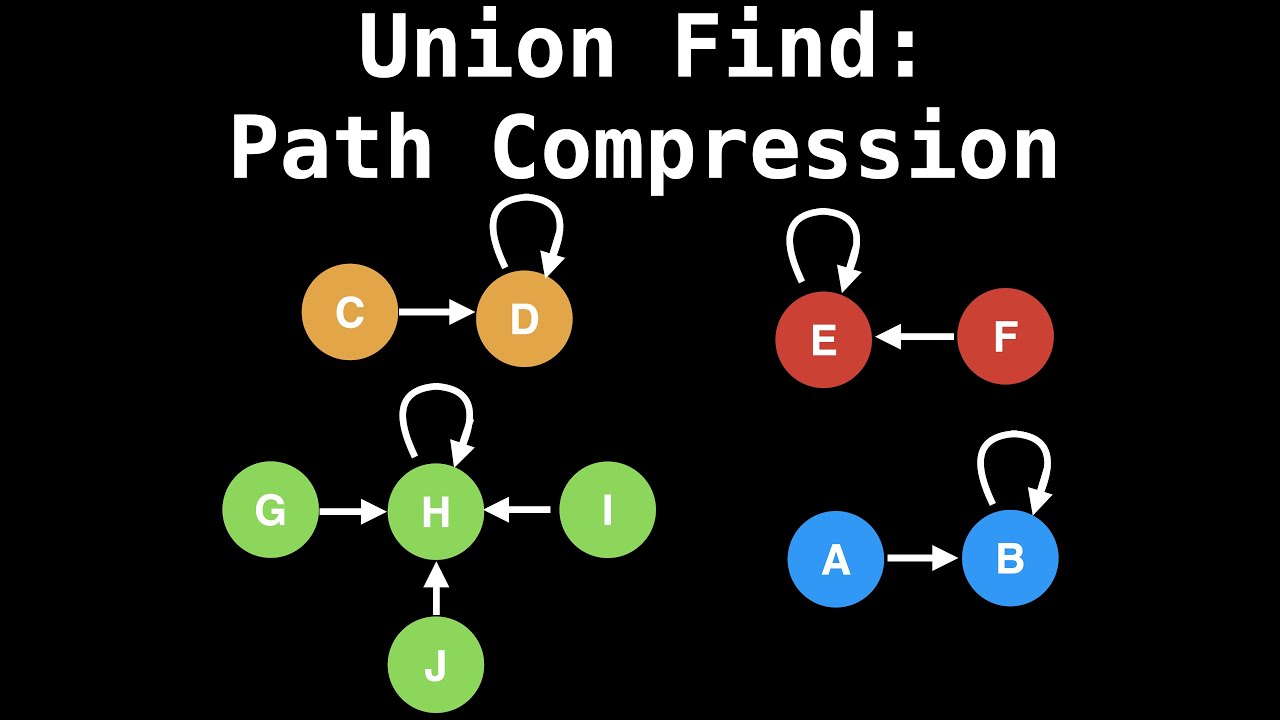
2.2 其他基于物理学原理的优化算法
2.2.1 引力搜索算法
受万有引力定律启发,学着提出了一种新型的群体智能优化算法——引力搜索算法(Gravitational Search Algorithm, GSA)。
万有引力定律:自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比,数学表达式为:
其中,$F$表示两个物体间的引力,$G$表示万有引力常数,$m_1$和$m_2$分别表示物体1和物体2的质量,$r$表示两个物体间的距离。
引力搜索算法在求解优化问题时,搜索个体的位置和问题的解相对应,个体质量用于评价个体的优劣,位置越好,质量越大。由于引力作用,个体之间相互吸引并且朝着质量较大的个体方向移动,个体运动遵循牛顿第二定律,随着运动不断进行,最终这个群体都会聚集在质量最大个体的周围,从而找到质量最大的个体,而质量最大的个体占据最优位置,因此算法可以获得问题的最优解。
算法流程如下图所示: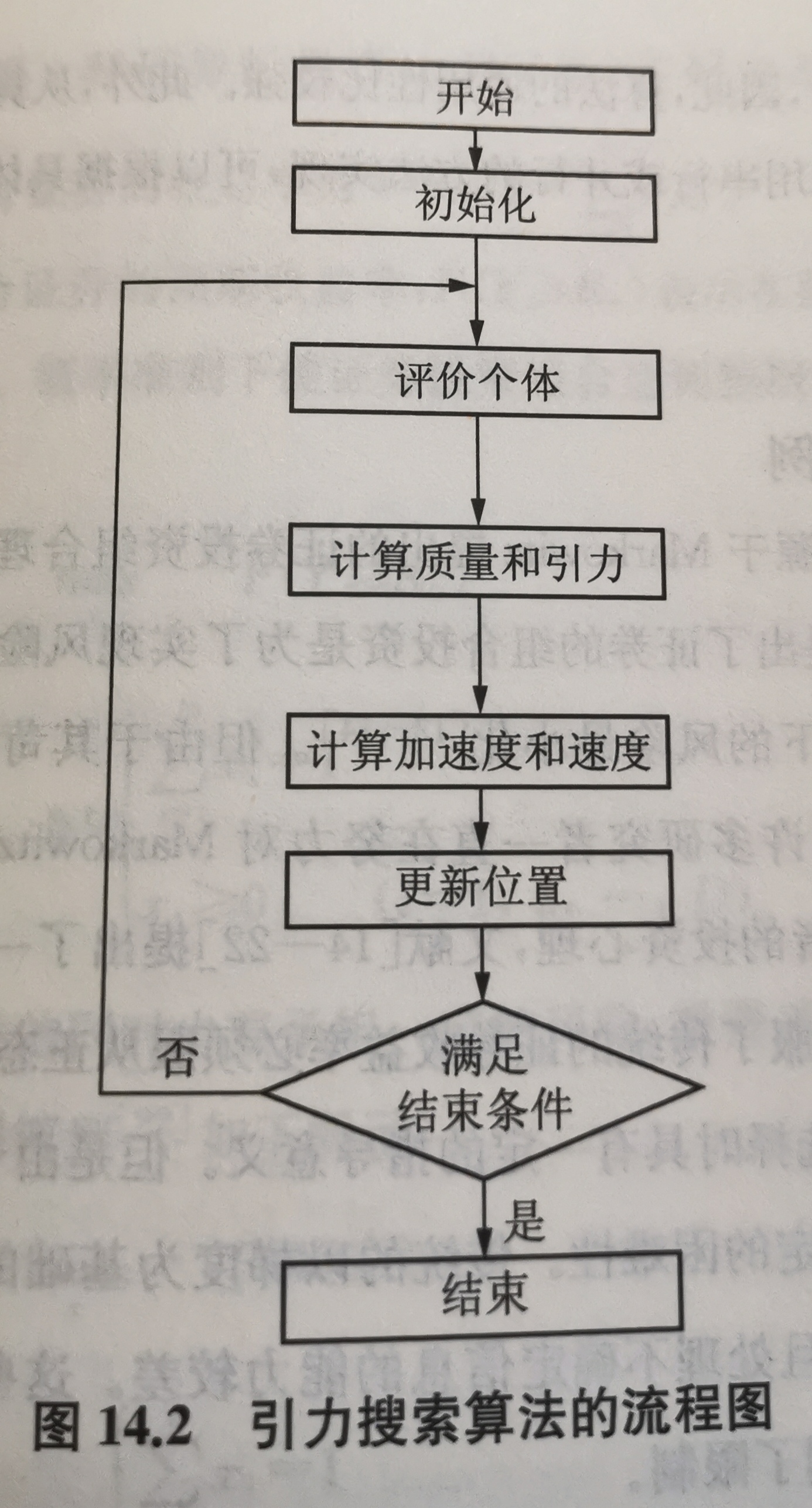
应用案例:
投资者偏好条件下概率准则投资组合问题
智能优化算法一般不要求目标函数连续性和可微性,甚至有时连有没有解析表达式都不要求,并且对计算中数据的不确定性也有很强的适应能力。
2.2.2 混沌优化算法
基于混沌现象(貌似无规律的复杂运动形态)的独特性质——遍历性、随机性以及规律性,我国学者李兵提出混沌优化算法,通过载波方法将混沌状态和决策变量相对应,然后将混沌运动的遍历范围映射到决策变量的的取值范围,最后利用混沌变量进行优化搜索。
混沌优化算法的几种特征:
- 初值敏感性
- 遍历性
- 规律性
- 随机性
算法基本步骤:
- 算法初始化。
- 第一次载波。
- 用混沌变量进行迭代搜索。
- 经过若干次搜索后优化目标函数值没有发生改变,进行第二次搜索。
- 运用二次载波后的混沌变量进行迭代搜搜。
- 满足终止条件,终止搜索;否则返回步骤5。
应用案例:
求解天体力学Kepler方程
2.2.3 随机分形搜索算法
随机分形搜索算法(Stochastic Fractal Search Algorithm, SFS)采用高斯随机游走模型,基于个体当前位置进行扩散,并根据适应度函数对个体位置做进一步更新。
分形:自相似性,部分与整体具有相似性,图案之中递归的套着图案。
随机分形搜索算法将微粒类比为寻优个体,扩散过程类比为优化过程,寻优个体的位置和待优化问题的解相对应,且个体位置的优劣将通过目标函数值的大小进行评价。
主要步骤:
- 设置算法参数,进行种群初始化
- 计算个体适应度函数值,找到当前最佳点BP
- 执行扩散过程,对于每一个扩散的个体,根据选择的高斯游走模型生成新个体的新位置
- 进行群体第一次更新
- 进行群体第二次更新
- 判断终止条件,不满足则执行步骤2
应用案例:
CEC2010测试函数库
2.2.4 光学优化算法
光学优化算法(Optics Inspired Optimization, OIO)2015年才提出,假设初始解为一系列初始光源点,经球面镜函数反射,得到相应的像点,这一系列像点,作为下一次搜索的光源点,不断反射搜索,即可找到最优解。
应用案例:
城市排水工程——暴雨强度公式参数优化
2.2.5 量子优化算法
量子计算(Quantum computing, QC),遇事不决,量子力学。
量子优化算法可以和很多优化算法结合,比如量子神经计算、量子遗传算法、量子退火算法等,与其他优化算法相比建模方式有所区别,编码方式也不同
应用案例:
VRP问题