2047. 句子中的有效单词数 [EASY]
句子仅由小写字母(’a’ 到 ‘z’)、数字(’0’ 到 ‘9’)、连字符(’-‘)、标点符号(’!’、’.’ 和 ‘,’)以及空格(’ ‘)组成。每个句子可以根据空格分解成 一个或者多个 token ,这些 token 之间由一个或者多个空格 ‘ ‘ 分隔。
如果一个 token 同时满足下述条件,则认为这个 token 是一个有效单词:
- 仅由小写字母、连字符和/或标点(不含数字)。
- 至多一个 连字符 ‘-‘ 。如果存在,连字符两侧应当都存在小写字母(”a-b” 是一个有效单词,但 “-ab” 和 “ab-“ 不是有效单词)。
- 至多一个 标点符号。如果存在,标点符号应当位于 token 的 末尾 。
这里给出几个有效单词的例子:”a-b.”、”afad”、”ba-c”、”a!” 和 “!” 。
给你一个字符串 sentence ,请你找出并返回 sentence 中 有效单词的数目 。
1 | /* |
2048. 下一个更大的数值平衡数 [MEDIUM]
如果整数 x 满足:对于每个数位 d ,这个数位 恰好 在 x 中出现 d 次。那么整数 x 就是一个 数值平衡数 。
给你一个整数 n ,请你返回 严格大于 n 的 最小数值平衡数 。
示例 1:
输入:n = 1
输出:22
解释:
22 是一个数值平衡数,因为:
- 数字 2 出现 2 次
这也是严格大于 1 的最小数值平衡数。
示例 2:
输入:n = 1000
输出:1333
解释:
1333 是一个数值平衡数,因为:
- 数字 1 出现 1 次。
- 数字 3 出现 3 次。
这也是严格大于 1000 的最小数值平衡数。
注意,1022 不能作为本输入的答案,因为数字 0 的出现次数超过了 0 。
示例 3:
输入:n = 3000
输出:3133
解释:
3133 是一个数值平衡数,因为:
- 数字 1 出现 1 次。
- 数字 3 出现 3 次。
这也是严格大于 3000 的最小数值平衡数。
提示:
0 <= n <= 1061
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64/*
审题:这题不会
暴力法先提交了一次,没过!
然后想貌似可以取巧,反正数字也不多,存到vector里查找就可以了,确实可以
看评论说暴力也能过,原来是因为我用的map(yydlj)
*/
// 暴力
#include <vector>
class Solution {
public:
bool isBeautifulNumber(int number) {
vector<int> bitCount(10, 0);
while (number > 0) {
int res = number % 10;
bitCount[res]++;
number /= 10;
}
for (int i = 0; i < 10; i++) {
if (bitCount[i] && bitCount[i] != i) {
return false;
}
}
return true;
}
int nextBeautifulNumber(int n) {
int number = n + 1;
while (!isBeautifulNumber(number)) {
++number;
}
return number;
}
};
// 打表
#include <unordered_map>
class Solution {
public:
bool isBeautifulNumber(int number) {
unordered_map<int, int> bitCount;
while (number > 0) {
int res = number % 10;
bitCount[res]++;
number /= 10;
}
for (auto& i : bitCount) {
if (i.first != i.second) {
return false;
}
}
return true;
}
int nextBeautifulNumber(int n) {
int number = n + 1;
vector<int> allLists = {1, 22, 122, 212, 221, 333, 1333, 3133, 3313, 3331, 4444, 14444, 22333, 23233, 23323, 23332, 32233, 32323, 32332, 33223, 33232, 33322, 41444, 44144, 44414, 44441, 55555, 122333, 123233, 123323, 123332, 132233, 132323, 132332, 133223, 133232, 133322, 155555, 212333, 213233, 213323, 213332, 221333, 223133, 223313, 223331, 224444, 231233, 231323, 231332, 232133, 232313, 232331, 233123, 233132, 233213, 233231, 233312, 233321, 242444, 244244, 244424, 244442, 312233, 312323, 312332, 313223, 313232, 313322, 321233, 321323, 321332, 322133, 322313, 322331, 323123, 323132, 323213, 323231, 323312, 323321, 331223, 331232, 331322, 332123, 332132, 332213, 332231, 332312, 332321, 333122, 333212, 333221, 422444, 424244, 424424, 424442, 442244, 442424, 442442, 444224, 444242, 444422, 515555, 551555, 555155, 555515, 555551, 666666, 1224444};
auto item = std::lower_bound(allLists.begin(), allLists.end(), number);
return *item;
}
};
2049. 统计最高分的节点数目 [MEDIUM]
给你一棵根节点为 0 的 二叉树 ,它总共有 n 个节点,节点编号为 0 到 n - 1 。同时给你一个下标从 0 开始的整数数组 parents 表示这棵树,其中 parents[i] 是节点 i 的父节点。由于节点 0 是根,所以 parents[0] == -1 。
一个子树的 大小 为这个子树内节点的数目。每个节点都有一个与之关联的 分数 。求出某个节点分数的方法是,将这个节点和与它相连的边全部 删除 ,剩余部分是若干个 非空 子树,这个节点的 分数 为所有这些子树 大小的乘积 。
请你返回有 最高得分 节点的 数目 。
示例 1: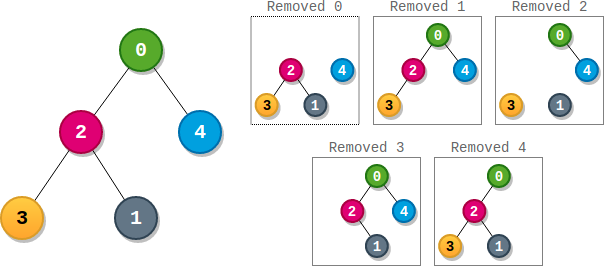
输入:parents = [-1,2,0,2,0]
输出:3
解释:
- 节点 0 的分数为:3 * 1 = 3
- 节点 1 的分数为:4 = 4
- 节点 2 的分数为:1 1 2 = 2
- 节点 3 的分数为:4 = 4
- 节点 4 的分数为:4 = 4
最高得分为 4 ,有三个节点得分为 4 (分别是节点 1,3 和 4 )。
示例 2: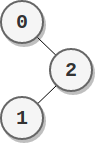
输入:parents = [-1,2,0]
输出:2
解释:
- 节点 0 的分数为:2 = 2
- 节点 1 的分数为:2 = 2
- 节点 2 的分数为:1 * 1 = 1
最高分数为 2 ,有两个节点分数为 2 (分别为节点 0 和 1 )。
提示:
- n == parents.length
- 2 <= n <= 105
- parents[0] == -1
- 对于 i != 0 ,有 0 <= parents[i] <= n - 1
- parents 表示一棵二叉树。
1 | 审题:看到题目理解了好久,想着要不要建树,但感觉又想到了不建的方法,但是要递归遍历好多次vector,纠结着就放弃了 |
2050. 并行课程 III [HARD]
给你一个整数 n ,表示有 n 节课,课程编号从 1 到 n 。同时给你一个二维整数数组 relations ,其中 relations[j] = [prevCoursej, nextCoursej] ,表示课程 prevCoursej 必须在课程 nextCoursej 之前 完成(先修课的关系)。同时给你一个下标从 0 开始的整数数组 time ,其中 time[i] 表示完成第 (i+1) 门课程需要花费的 月份 数。
请你根据以下规则算出完成所有课程所需要的 最少 月份数:
如果一门课的所有先修课都已经完成,你可以在 任意 时间开始这门课程。
你可以 同时 上 任意门课程 。
请你返回完成所有课程所需要的 最少 月份数。
注意:测试数据保证一定可以完成所有课程(也就是先修课的关系构成一个有向无环图)。
示例 1:
输入:n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
输出:8
解释:上图展示了输入数据所表示的先修关系图,以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 和 2 。
课程 1 花费 3 个月,课程 2 花费 2 个月。
所以,最早开始课程 3 的时间是月份 3 ,完成所有课程所需时间为 3 + 5 = 8 个月。
示例 2: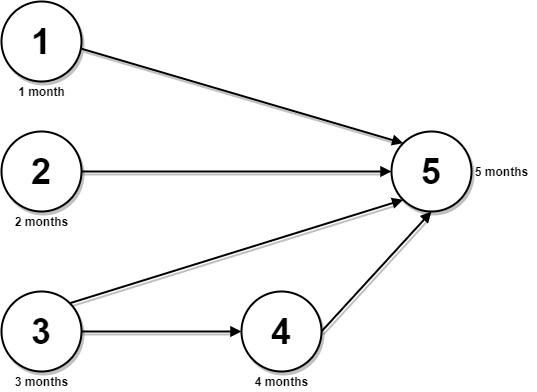
输入:n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
输出:12
解释:上图展示了输入数据所表示的先修关系图,以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 ,2 和 3 。
在月份 1,2 和 3 分别完成这三门课程。
课程 4 需在课程 3 之后开始,也就是 3 个月后。课程 4 在 3 + 4 = 7 月完成。
课程 5 需在课程 1,2,3 和 4 之后开始,也就是在 max(1,2,3,7) = 7 月开始。
所以完成所有课程所需的最少时间为 7 + 5 = 12 个月。
提示:
- 1 <= n <= 5 * 104
- 0 <= relations.length <= min(n (n - 1) / 2, 5 104)
- relations[j].length == 2
- 1 <= prevCoursej, nextCoursej <= n
prevCoursej != nextCoursej - 所有的先修课程对 [prevCoursej, nextCoursej] 都是 互不相同 的。
- time.length == n
- 1 <= time[i] <= 104
- 先修课程图是一个有向无环图。
1 | 审题:排序后,合并区间比如[3,4], [4,5]先合成[3,5],然后分层级取每层最大值,比如例2分3层,1,2,3为一层,最大值为3,4为第二层,最大值为4,5为第三层,最大值为5,加起来12。但是合并已经比较麻烦,分层也很难,比如遇到两个区间,[1, 2, 4]和[2, 3, 4],需要继续合并,然后成为[1,2,3,4],还是有点难 |