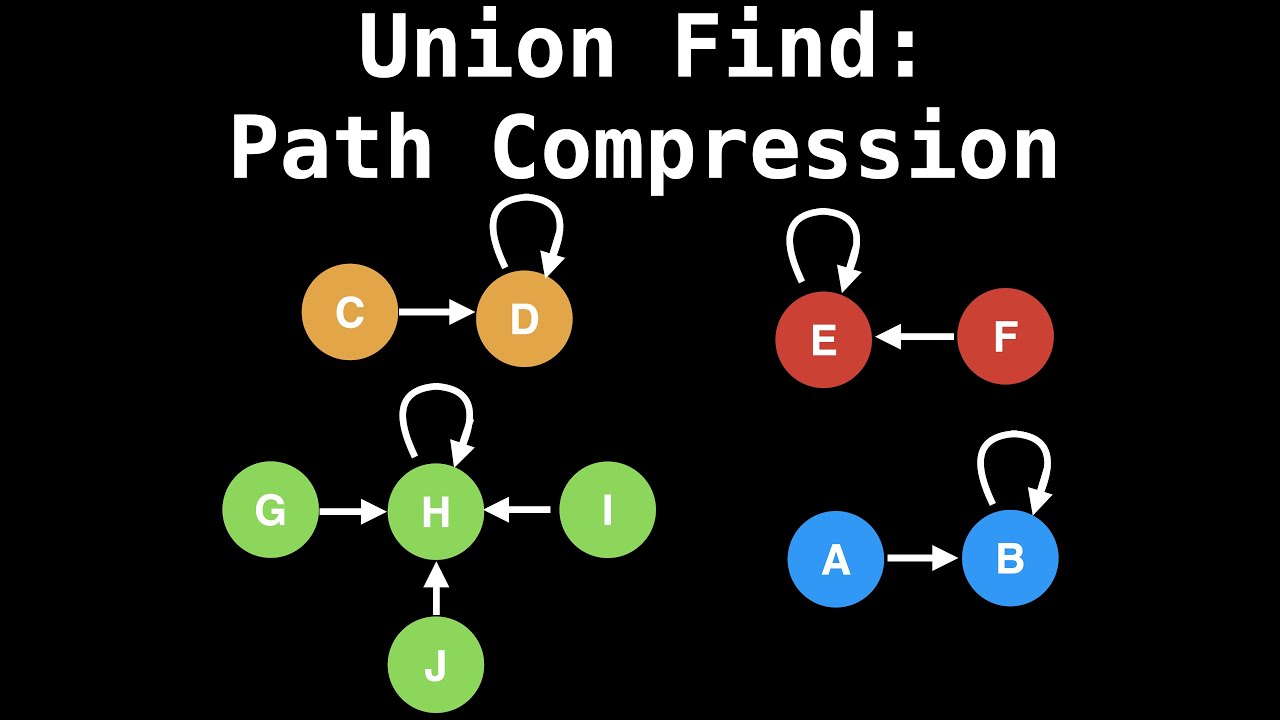
通用模板,路径压缩
应用场景
- 克鲁斯卡尔最小生成树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54template <class T>
class UF {
public:
// n 为图中节点的个数
explicit UF(int n)
{
count_ = n;
parent_ = new T[n];
for (T i = 0; i < n; i++) {
parent_[i] = i;
}
}
// 将节点 p 和节点 q 连通
void Union(T p, T q) {
T rootP = Find(p);
T rootQ = Find(q);
if (rootP == rootQ) {
return;
}
parent_[rootQ] = rootP;
// 两个连通分量合并成一个连通分量
count_--;
}
// 判断节点 p 和节点 q 是否连通
bool Connected(T p, T q) {
T rootP = Find(p);
T rootQ = Find(q);
return rootP == rootQ;
}
// 返回图中的连通分量个数
[[nodiscard]] int Count() const {
return count_;
}
// 返回节点 x 的连通分量根节点
private:
T Find(T x) {
while (parent_[x] != x) {
// 进行路径压缩
parent_[x] = parent_[parent_[x]];
x = parent_[x];
}
return x;
}
// 连通分量个数
int count_;
// 存储每个节点的父节点
T* parent_;
};
990. 等式方程的可满足性
1 | class Solution { |